Модель ценообразования CAPM
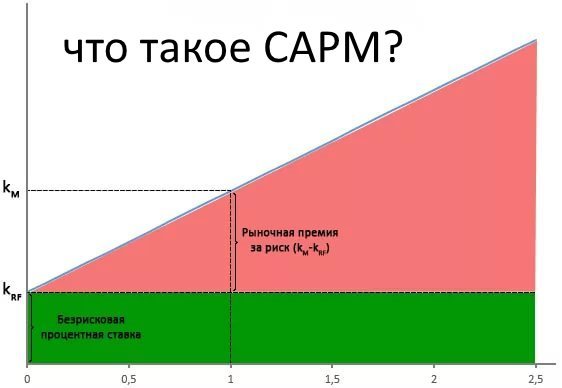
Математической основой инвестиционного портфеля является теория ценообразования активов (Capital Asset Pricing Model, САРМ), которая тесно связана с теорией Марковица. Если пытаться говорить простыми словами, то CAPM разделяет весь рыночный риск на две части: так называемую безрисковую составляющую и коэффициент бета.
Последний называется систематическим (недиверсифицируемым) риском и является столпом теории. Не систематический (диверсифицируемый) риск убирается в теории Марковица путем диверсификации портфеля по нескольким активам (видам активов) и рассмотрения риска портфеля в общем, а не каждого отдельного компонента. Предпосылки CAPM дают следующую формулу:
Ce = Cf + β (Cm-Cf), где
- Се – доходность выбранной акции;
- Cf – доходность безрисковых вложений;
- β – коэффициент, рассчитываемый для каждой акции;
- Cm – уровень доходности на рынке ценных бумаг
Спорным для интерпретации оказывается коэффициент Cf. При работе на американском рынке за него обычно принимается доходность казначейских облигаций за сроки от года до 10 лет. В условиях России даже государственные облигации далеко не все согласны считать безрисковыми, вспоминая ГКО; тем не менее, в качестве альтернативы можно предложить лишь ставку по депозитам Сбербанка или вовсе отказаться от данной методики.
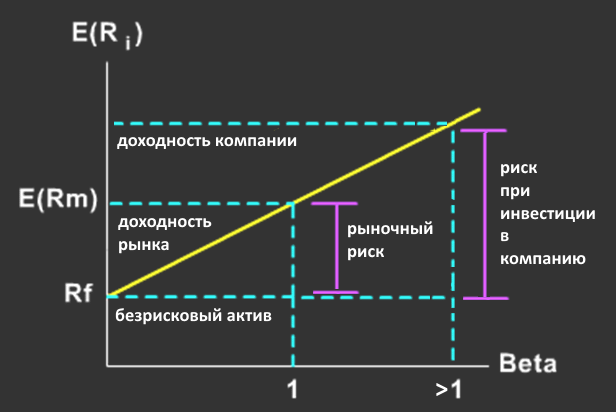
Коэффициент бета показывает отношение доходности данного актива по отношению к доходности в среднем на рынке ценных бумаг и может быть рассчитан по котировкам компании. Стоит также напомнить, что в целом по рынку коэффициент β равен единице; меньшая величина в рамках теории показывает меньший риск эмитента, чем в среднем по рынку, тогда как значение, большее 1, говорит о повышенном риске.
Коэффициент зависит от времени и принимается константой только на выбранном временном промежутке; его увеличение со временем говорит о том, что актив компании начал нести больше риска (и наоборот). Теория исходит из ликвидности всех активов, отсутствия издержек на транзакции и нулевого налогообложения. Для ясности можно привести три примера.
Пример 1
Попробуем по модели CAPM вычислить справедливую доходность акции российского рынка. Возьмем в качестве безрисковой составляющей актуальную ставку Сбербанка – для вклада “Сохраняй” сроком в 1-2 года на сегодняшний день она равна 6.1%. Средняя геометрическая доходность индекса ММВБ с сентября 1997 года по июнь 2016 равна 17% годовых.
Теперь выберем какую-либо компанию Х и поищем в ее описании бета-коэффициент, который считается по двум массивам данных: доходности акции и индекса сравнения. Если коэффициент не указан, то можно рассчитать его самому. Получить котировки российских акций можно на сайте finam.ru в разделе «Про рынок» → «Экспорт данных».
Более простой вариант это воспользоваться ссылкой https://ru.investing.com/stock-screener/ или сервисом Finviz для акций США. В первом случае коэффициент бета отображается за годовой период:
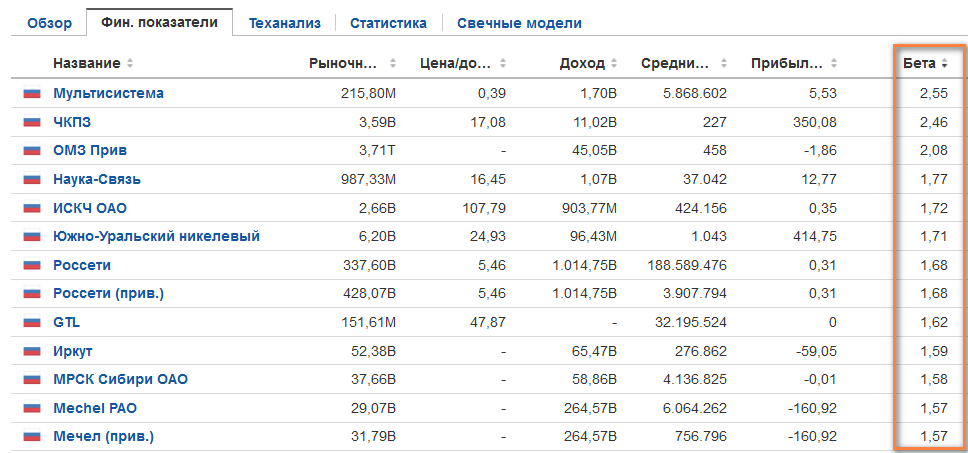
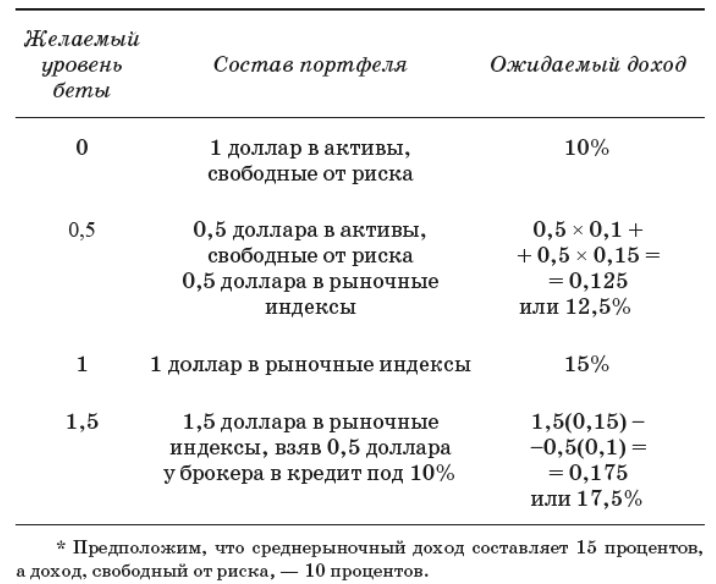
Допустим, что у нас β = 0.5. Тогда
Ce = Cf + β (Cm-Cf) = 6.1 + 0.5 (17 – 6.1) = 11.55%
Разницу между Ce и Cf можно считать компенсацией риска (премией за рыночный риск). Мы получили конкретную доходность – она ниже среднерыночной, но при этом достигнута с риском в два раза меньшим, чем у индекса. Инвестор вправе решать, включать ли акцию с таким ожидаемым доходом в свой портфель.
Пример 2
Даны две компании. Пусть компания А имеет β = 1.6, а у компании В коэффициент β = 0.9. Возьмем безрисковую ставку на уровне 6%, а среднюю доходность на рынке ценных бумаг снова 17%. Тогда
Для компании А: Се = 6 + 1,6 × (17-6) = 23,6%
Для компании В: Се = 6 + 0,9 × (17-6) = 15,9%
Расчет очевидным образом дает более высокие значения прибыли для той компании, коэффициент бета которой больше. Но значит ли это, что инвестирование в первую компанию непременно даст более высокую доходность? Нет, поскольку модель подходит к компании по принципу “черного ящика” – через коэффициент бета она учитывает историю доходности компании, но ничего не говорит о текущей и будущей ситуации в ней.
Следовательно, для принятия инвестиционного решения можно дополнительно воспользоваться фундаментальным анализом – сравнив, например, такие показатели как P/E, PEG Ratio, чистую маржу, коэффициент рентабельности активов и др. исследуемой компании с другими подобными ей или со средними значениями по отрасли. Тем не менее и это может не принести результат.
Пример 3
Модель исходит из линейной корреляции доходности и риска при одновременной оценке портфеля из нескольких компаний, что проще всего показать следующим расчетом:
Пусть портфель включает следующие активы со средней доходностью: А (14%); В (28%); С (35%); D (13%); Е (10%). Коэффициент бета составляет соответственно: А (1,3); В (1,6); С (0,7); D (0,9); Е (1). Найти средний коэффициент бета.
Решение: β (среднее) = 0,14 × 1,3 + 0,28 × 1,6 + 0,35 × 0,7 + 0,13 × 0,9 + 0,1 × 1 = 1,092
Выводы
Несмотря на формализм, теория САРМ позволяет произвести первичную оценку как отдельной компании, так и инвестиционного портфеля. Кроме того, она вводит такое распространенное понятие, как бета-коэффициент. Его значение может сказать нам, идет ли речь о компании роста (β > 1) или о компании стоимости (β < 1), результаты инвестирования в которые до сих пор является предметом оживленных дебатов.
Однако CAPM лишь ограничивается общим утверждением, что с возрастанием β увеличивается и риск – но не считает его количественно в виде среднеквадратичного отклонения, как в теории Марковица. Т.е. по сути CAPM не видит, с какой волатильностью был получен доход, лишь сравнивая его со средним по рынку. Кроме того, при оценке нескольких активов не учитывается их взаимная корреляция, которая по Марковицу позволяет в ряде случаев получать больший доход с меньшим риском, чем у каждого компонента в отдельности.
Доходность инвестиций в Газпромбанк — это показатель, который отражает прибыль, полученную от вложений в различные финансовые инструменты, такие как акции, облигации, паевые инвестиционные фонды (ПИФы), а также другие инвестиционные продукты, предлагаемые Газпромбанком. Этот показатель измеряет эффективность вложений и позволяет инвестору оценить, насколько успешно его капитал работает на протяжении определенного времени.
Как рассчитывается доходность инвестиций?
Доходность инвестиций может быть рассчитана разными методами в зависимости от типа вложений, но основной формулой для расчета является:
Доходность=(Конечнаястоимостьинвестиций−Начальнаястоимость)+ДивидендыилипроцентыНачальнаястоимость×100%\text{Доходность} = \frac{(Конечная стоимость инвестиций - Начальная стоимость) + Дивиденды или проценты}{Начальная стоимость} \times 100\%
- Конечная стоимость инвестиций — это сумма, которую инвестор получает по завершении инвестиционного периода.
- Начальная стоимость — это сумма, которую инвестор вложил на начальном этапе.
- Дивиденды или проценты — это доход, полученный от вложений (например, дивиденды по акциям или проценты по облигациям).